Que cherchons-nous ? : Le définition de numérisation afin d’avoir un fichier optimal par rapport à l’utilisation que l’on veut en faire…

Pour commencer, posons le problème en nous aidant du croquis suivant :

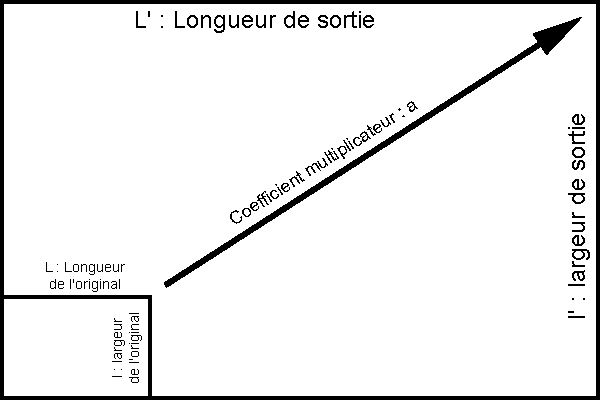
Nous avons donc un document (Tirage photographique, négatif, diapositive…) original dont les dimensions sont Longueur par largeur ( Soit L x l ).
Et nous voulons obtenir une image de sortie dont les dimensions seront Longueur prime par largeur prime ( Soit L’ x l’ ).

On appliquera donc un coefficient multiplicateur ( a ) pour passer de l’original au document de sortie.

Nous avons donc posé la base de notre travail, maintenant, il faut définir le support de sortie du document final.

Je vous donne ici trois type de sortie :

• Sortie impression jet d’encre ;
• Sortie tirage numérique, type Fuji Frontier ;
• Sortie écran, affichage internet / e-mail.

Par rapport à ces périphériques de sortie, il faut impérativement connaître la définition dont ils ont besoin.
Je vais alors reprendre les trois exemples ci-dessus :

• Jet d’encre : Définition entre 150 et 200 dpi ou ppp ( dpi : dots per inch ou ppp : points par pouce ), par défaut, je prends 200 dpi, prendre plus n’est pas intéressant dans la mesure où l’on ne verra pas, visuellement, la différence, et que l’on va travailler avec un fichier plus lourd, ce qui va nous prendre plus de temps ;
• Tirage photo numérique : Ici, nous n’avons pas le choix, c’est 300 dpi. / !\ pas 299 ou 301 dpi mais impérativement 300 !
• Ecran : la définition moyenne d’un écran est de 72 dpi, on voit bien que cette définition est assez médiocre, mais adaptée aux moniteurs.

Voila, nous avons tous les éléments pour définir la définition de numérisation ( D ) dont la formule est très simple :

où le coefficient multiplicateur est défini par la formule suivante :

Pour imager cela, prenons un exemple :

• Nous voulons numériser un négatif 24x36,
• que nous voulons agrandir à un format de 20x30cm,
• via une tireuse numérique.

Pour "agrandir" notre image, nous devons "aller" de 24 mm à 200 mm. Ce qui nous donne : a = l’ / l = 200 / 24 = 8,33.
On peut donc en déduire la définition de numérisation D = définition du support de sortie x coefficient multiplicateur (a) = 300 x 8,33 = 2499.

Il nous faut donc un scanner (ici un scanner de film) qui nous permette de numériser à un définition d’au moins 2500 dpi pour pouvoir faire un tel agrandissement…